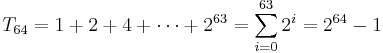Wheat and chessboard problem
| a | b | c | d | e | f | g | h | ||
| 8 | 8 | ||||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h |
The wheat and chessboard problem (the problem is sometimes expressed in terms of rice instead of wheat) is a mathematical problem:
If a chessboard were to have wheat placed upon each square such that one grain were placed on the first square, two on the second, four on the third, and so on (doubling the number of grains on each subsequent square), how many grains of wheat would be on the chessboard at the finish?
To solve this, observe that a chess board is an 8×8 square, containing 64 squares. If the amount of grains doubles on successive squares, then the sum of grains on all 64 squares is:
This equals 18,446,744,073,709,551,615 (18.4 quintillion).
This problem (or a variation of it) demonstrates the quick growth of exponential sequences.
Contents |
Origin of the problem
While the story behind the problem changes from person to person, the fable usually follows the same idea:
When the creator of the game of chess (in some tellings an ancient Indian mathematician, in others a legendary dravida vellalar named Sessa or Sissa) showed his invention to the ruler of the country, the ruler was so pleased that he gave the inventor the right to name his prize for the invention. The man, who was very wise, asked the king this: that for the first square of the chess board, he would receive one grain of wheat (in some tellings, rice), two for the second one, four on the third one, and so forth, doubling the amount each time. The ruler, arithmetically unaware, quickly accepted the inventor's offer, even getting offended by his perceived notion that the inventor was asking for such a low price, and ordered the treasurer to count and hand over the wheat to the inventor. However, when the treasurer took more than a week to calculate the amount of wheat, the ruler asked him for a reason for his tardiness. The treasurer then gave him the result of the calculation, and explained that it would be impossible to give the inventor the reward. The ruler then, to get back at the inventor who tried to outsmart him, cut off the inventor's head to discourage such trickery.
Variations
The problem also has another setting, the Roman Empire. When a brave general came back to Rome, the Cæsar asked him to name a price for the services he had offered to his country. When the general asked for an exorbitant price, the Caesar, not wanting to sound cheap, or that he was going to go back on his word, made him an offer; the next day, the general was to go to the treasury, and grab a one gram gold coin, the next day, a two gram gold coin, and each day, the weight of the coin would double, and the general could take it, as long as he was able to carry it by himself. The general, seeing a good opportunity to make money quickly, agreed. However, by the end of the 18th day, the general was not able to carry any more coins. The general only received a small fraction of what he had asked the Caesar. Yakov Perelman retells the story in one of his books with brass coins instead of gold ones, starting with five gram. The general manages to take 17 coins, and the last two must be rolled in instead of being carried.
Another version places two merchants together. One merchant offers the other a deal; that for the next month, the merchant was going to give $10,000 (or, in some variants, even $100,000) to the other one, and in return, he would receive 1 cent the first day, 2 cents the second, 4 cents on the third, and so on, each time doubling the amount. The second merchant agreed, and for the first three weeks (or more, depending on the variant), he enjoyed the fortunes that the first merchant was "unwittingly" giving him, but by the end of the month, the second merchant was broke, while the first merchant was incredibly rich.
Yet another variant is about a man buying a horse and displeased with the high price. The owner offers him to buy it by paying instead one cent for the first nail in its horseshoes, two for the second nail, and so on. With each horseshoe having six nails, the results are similar to the above story.
Some books about popular mathematics also mention this problem: Fold a Post-it note in half seven times, and then try to rip the note. Folding the paper would soon become difficult as the note becomes increasingly smaller and increasingly harder to manipulate. However, even if you were to start with a large piece of paper, you would be unable to rip it because the paper would be 128 sheets thick.
Second half of the chessboard
In technology strategy, the second half of the chessboard is a phrase, coined by Ray Kurzweil[2], in reference to the point where an exponentially growing factor begins to have a significant economic impact on an organization's overall business strategy.
While the number of grains on the first half of the chessboard is large, the amount on the second half is vastly larger.
The number of grains of rice on the first half of the chessboard is 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 512 + 1024 + ... + 2,147,483,648, for a total of 232 − 1 = 4,294,967,295 grains of rice, or about 100,000 kg of rice, with the mass of one grain of rice taken as 25 mg.[1] This amount is about 1/1,200,000 of total rice production in India per annum (in 2005).[2]
The number of grains of rice on the second half of the chessboard is 232 + 233 + 234 ... + 263, for a total of 264 − 232 grains of rice (the square of the number of grains on the first half of the board plus itself). Indeed, as each square contains one grain more than the total of all the squares before it, the first square of the second half alone contains more grains than the entire first half.
On the 64th square of the chessboard alone there would be 263 = 9,223,372,036,854,775,808 grains of rice, or more than two billion times as much as on the first half of the chessboard.
On the entire chessboard there would be 264 − 1 = 18,446,744,073,709,551,615 grains of rice, weighing 461,168,602,000 metric tons, which would be a heap of rice larger than Mount Everest. This is around 1,000 times the global production of rice in 2010 (464,000,000 metric tons).[3]
See also
References
- ^ Raymond Kurzweil (1999). The Age of Spiritual Machines. Viking Adult. ISBN 0-670-88217-8.
- ^ "Internet Archive Wayback Machine". Web.archive.org. 2006-08-23. http://web.archive.org/web/20060823025557/http://www.ricecrc.org/reader/tg_Size_and_Weight.htm. Retrieved 2011-09-16.
- ^ [1]
- ^ World rice output in 2011 estimated at 476 mn tonnes: FAO
External links
- Weisstein, Eric W., "Wheat and Chessboard Problem" from MathWorld.
- One telling of the fable
- Salt and chessboard problem - A variation on the wheat and chessboard problem with measurements of each square.